Είναι το Coin Flip πραγματικά Fifty-Fifty;

Μια αναστροφή νομίσματος είναι η πεμπτουσία των πενήντα πενήντα πιθανοτήτων, αλλά μια μεγάλη ομάδα ερευνητών πρόσφατα


ανέτρεψε τη δίκαιη φήμη της


. Καταγράφοντας ένα επίπονο χτύπημα 350.000+ νομισμάτων με το χέρι, διαπίστωσαν ότι σχεδόν το 51% των πετάξεων προσγειώνεται με την ίδια πλευρά στραμμένη προς τα πάνω όπως πριν από το χτύπημα (δηλ. αν το κέρμα δείχνει κεφάλια στην αρχή όταν σκαρφαλώνει στον αντίχειρά σας, τότε είναι πιο πιθανό να προσγειωθούν κεφάλια, και το ίδιο ισχύει για τις ουρές). Αν ψάχνετε για το επόμενο ρολόι σας, οι ερευνητές μαγνητογράφησαν κάθε αναστροφή και έκαναν το βίντεο


δημόσια διαθέσιμο


.

Με τόσα πολλά σημεία δεδομένων, τα αποτελέσματα είναι στατιστικά σημαντικά και προκαλούν για πάντα ένα πλήγμα στα bar στοιχήματα και στα εναρκτήρια NFL. Ευτυχώς, η ομάδα δοκίμασε μια ποικιλία νομισμάτων και δεν βρήκε προτίμηση για κεφάλια έναντι ουρών. Έτσι, μπορείτε να αποκαταστήσετε την ιερότητα μιας δίκαιης ρίψης νομίσματος αποκρύπτοντας τον αρχικό προσανατολισμό του από το άτομο που το καλεί.

Το να γυρίζεις ένα κέρμα φαίνεται ακόμα χειρότερο.


Μερικοί




δουλειά


έχει διαπιστώσει ότι οι πένες που γυρίζουν είναι πολύ πιο πιθανό να προσγειωθούν. Την επόμενη φορά που ο φίλος σας θα θελήσει να διευθετήσει κάτι γυρίζοντας ένα νόμισμα, ίσως προτείνετε να γυρίσετε μια δεκάρα. Θυμηθείτε να καλέσετε ουρές.

Σου έλειψε το παζλ της περασμένης εβδομάδας; Τσέκαρέ το



εδώ



, και βρείτε τη λύση του στο κάτω μέρος του σημερινού άρθρου. Προσέξτε να μην διαβάσετε πολύ μπροστά, αν δεν έχετε λύσει ακόμα την προηγούμενη εβδομάδα!

Παζλ #27: Το κεφάλι ψηλά

Εσύ κι εγώ θα διευθετήσουμε κάτι με μια ανατροπή του νομίσματος. Αντί για μια συνηθισμένη αναστροφή νομίσματος, θα καλέσετε είτε “HHT” ή “THH”. Στη συνέχεια, θα γυρίσουμε το κέρμα πολλές φορές στη σειρά και θα καταγράψουμε τα αποτελέσματα. Εάν η αλληλουχία κεφαλές, κεφαλές, ουρές εμφανιστεί πρώτα, τότε κερδίζει το HHT και εάν εμφανιστεί πρώτη η ακολουθία ουρές, κεφαλές, κεφαλές, τότε κερδίζει το THH. Συνεχίζουμε να γυρίζουμε μέχρι να εμφανιστεί ένα από αυτά.

Ποιο καλείς; Ή δεν έχει σημασία;

Ποια είναι η πιθανότητα να κερδίσει ο καθένας;

Το νόμισμα είναι δίκαιο και είναι εξίσου πιθανό να σηκώσει τα κεφάλια ή τις ουρές σε κάθε δεδομένο χτύπημα.

Θα επιστρέψω την επόμενη Δευτέρα με την απάντηση και ένα

νέο

παζλ. Ξέρετε ένα ωραίο παζλ που πιστεύετε ότι πρέπει να εμφανίζεται εδώ; Στείλτε μου μήνυμα στο Twitter


@JackPMurtagh


ή στείλτε μου email στο

gizmodopuzzle@

gmail

.com

Λύση στο παζλ #26: Horsing Around

Πέρασες την προηγούμενη εβδομάδα

Ερώτηση συνέντευξης Google

?

Ένας στάβλος έχει 25 άλογα. Μπορείτε να αγωνιστείτε

πέντε

άλογα της επιλογής σας κάθε φορά και μάθετε ποιος κέρδισε, ποιος ήρθε δεύτερος, κλπ. Δεν μαθαίνετε πόσο γρήγορα έτρεξαν, μόνο τι θέση πήραν τα πέντε άλογα μεταξύ τους.

Ποιος είναι ο ελάχιστος αριθμός ιπποδρομιών που θα χρειαστείτε για να προσδιορίσετε τα τρία ταχύτερα άλογα από τα 25;

Θα χρειαστείτε επτά αγώνες. Φωνάζω σε

Lions-Eye Sea-Rear

για να συνοδεύσετε τη σωστή λύση σας με ένα ωραίο οπτικό βοήθημα.

Όταν έθεσα το πρόβλημα, είπα ότι δεν χρειάζεται να ανακαλύψετε τη σειρά κατάταξης των πιο γρήγορων τριών. Αρκετοί από εσάς επισημάνατε σωστά ότι η λύση με επτά αγώνες

κάνει

επίσης να σας πω τη σειρά των τριών πρώτων. Αυτό ήταν παράλειψη και ζητώ συγγνώμη αν η περιττή διευκρίνιση μου παραπλάνησε κάποιον από εσάς.

Δείτε πώς να το κάνετε σε επτά αγώνες. Κάθε άλογο χρειάζεται να συμμετάσχει σε μια κούρσα κάποια στιγμή, γιατί αν αφήσετε ένα άλογο χωρίς δοκιμή, δεν θα μάθετε ποτέ αν ήταν στην πρώτη τριάδα ή όχι. Ξεκινήστε λοιπόν με πέντε κούρσες όπου κάθε άλογο συμμετέχει σε μία από αυτές. Μαθαίνετε τα αποτελέσματα των ιπποδρομιών και μπορείτε να φτιάξετε έναν πίνακα σαν αυτόν, όπου κάθε γράμμα αντιπροσωπεύει ένα διαφορετικό άλογο.

Κάθε άλογο που πήρε την 4η ή 5η θέση στην κούρσα του μπορεί να εξαλειφθεί από την εξέταση γιατί ήδη γνωρίζουμε τρία άλογα που είναι ταχύτερα από αυτά. Για παράδειγμα, το άλογο N δεν μπορεί να είναι ένα από τα τρία ταχύτερα άλογα επειδή τα άλογα K, L και M είναι όλα πιο γρήγορα από το N (όλοι νικούν τον N στην κούρσα 4). Το Horse R, από την άλλη, θα μπορούσε να είναι στην πρώτη τριάδα, γιατί απ’ ό,τι ξέρουμε τα P, Q και R είναι τα τρία ταχύτερα άλογα. Δεν έχουμε αποδείξεις για το αντίθετο μέχρι να διεξαγάγουμε περαιτέρω αγώνες.

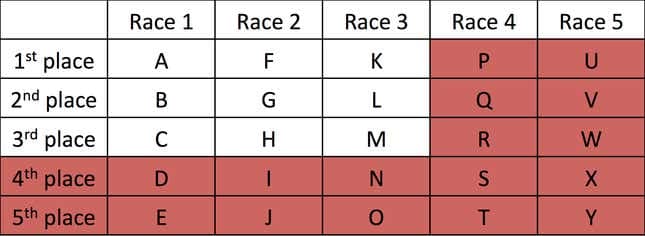
Για την 6η κούρσα μας, θα συγκρίνουμε τα πέντε άλογα που πήραν την πρώτη θέση στην αντίστοιχη κούρσα τους, δηλαδή θα βάλουμε τα άλογα A, F, K, P και U μεταξύ τους. Ας υποθέσουμε ότι τα αποτελέσματα είναι με αλφαβητική σειρά:

A > F > K > P > U (το A παίρνει πρώτο, το F παίρνει δεύτερο, και ούτω καθεξής).

Τώρα μπορούμε να εξαλείψουμε τα άλογα P και U από τη διαμάχη επειδή γνωρίζουμε τρία άλογα που είναι ταχύτερα από τα P και U (A, F και K).

Επιπλέον

, μπορούμε να εξαλείψουμε κάθε άλογο που έχει χάσει μια κούρσα από τον P και τον U (εάν ο P δεν φτάσει στην πρώτη τριάδα, τότε σίγουρα ένα άλογο που χάνει από τον P δεν το κάνει).

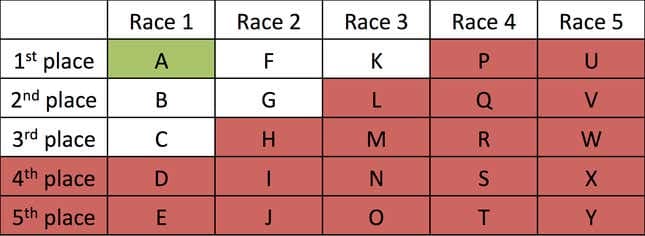
Η φυλή 6 μας επιτρέπει επίσης να εξαλείψουμε τα άλογα H, L και M επειδή μπορούμε να αναφέρουμε τρία άλογα που είναι ταχύτερα από αυτά. Για παράδειγμα, ο L χάνει από τον Κ (Κούρσα 3) και ο Κ χάνει από τον Α και τον Φ (Κούρσα 6). Ο αγώνας 6 μας δίδαξε επίσης ότι το Α είναι το πιο γρήγορο άλογο από όλα. Πώς το ξέρουμε αυτό; Θα μπορούσε το G να είναι πιο γρήγορο από το Α, για παράδειγμα; Όχι, γιατί το Α είναι πιο γρήγορο από το F (αγώνα 6) και το F είναι πιο γρήγορο από το G (αγώνα 2). Άλογο Μια νικηφόρα πρώτη θέση ανάμεσα στα άλογα της πρώτης θέσης τον στέφει τον γενικό νικητή, αλλά πρέπει ακόμα να βρούμε τα δύο επόμενα.

Ευτυχώς, απομένουν μόνο πέντε άλογα για δοκιμή, ώστε να μπορούμε να μάθουμε το δεύτερο και το τρίτο ταχύτερο άλογο συγκρίνοντας τα B, C, F, G και K στην Κούρσα 7.